Dans tout système de mesure, de la communication sans fil à la photographie numérique, le rapport signal sur bruit (RSB) est un critère de qualité fondamental. Que vous analysiez des images de télescope, amélioriez des enregistrements de microphone ou dépanniez une liaison sans fil, le RSB vous indique la quantité d'informations utiles qui se démarque du bruit de fond indésirable.
Cependant, calculer correctement le rapport signal/bruit (SNR) n'est pas toujours simple. Selon le système, des facteurs supplémentaires tels que le courant d'obscurité, le bruit de lecture ou le binning des pixels peuvent être à prendre en compte. Ce guide vous présente la théorie, les formules de base, les erreurs courantes, les applications et les solutions pratiques pour améliorer le SNR, vous permettant ainsi de l'appliquer avec précision dans un large éventail de contextes.
Qu'est-ce que le rapport signal sur bruit (SNR) ?
À la base, le rapport signal/bruit mesure la relation entre la force d’un signal souhaité et le bruit de fond qui l’obscurcit.
● Signal = l’information significative (par exemple, une voix dans un appel, une étoile dans une image de télescope).
● Bruit = fluctuations aléatoires et indésirables qui déforment ou masquent le signal (par exemple, statique, bruit du capteur, interférence électrique).
Mathématiquement, le SNR est défini comme :
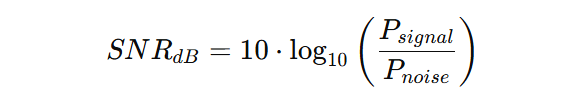
Étant donné que ces rapports peuvent varier sur plusieurs ordres de grandeur, le SNR est généralement exprimé en décibels (dB) :
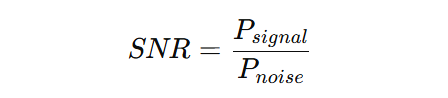
● Rapport signal/bruit élevé (par exemple, 40 dB) : le signal domine, ce qui donne des informations claires et fiables.
● Faible rapport signal/bruit (par exemple, 5 dB) : le bruit écrase le signal, rendant l'interprétation difficile.
Comment calculer le SNR
Le calcul du rapport signal sur bruit peut être effectué avec différents niveaux de précision selon les sources de bruit incluses. Cette section présente deux formes de calcul : l'une prenant en compte le courant d'obscurité, l'autre supposant qu'il peut être négligé.
Remarque : L’addition de valeurs de bruit indépendantes nécessite leur addition en quadrature. Chaque source de bruit est élevée au carré, additionnée et la racine carrée du total est calculée.
Rapport signal/bruit avec courant d'obscurité
Voici l’équation à utiliser dans les situations où le bruit du courant d’obscurité est suffisamment important pour nécessiter une inclusion :
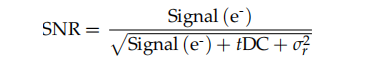
Voici la définition des termes :
Signal (e-) : Il s'agit du signal d'intérêt dans les photoélectrons, avec le signal de courant d'obscurité soustrait
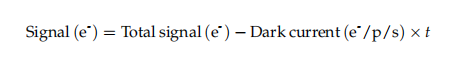
Le signal total (e-) correspond au nombre de photoélectrons dans le pixel d'intérêt, et non à sa valeur en niveaux de gris. La seconde occurrence du signal (e-), en bas de l'équation, correspond au bruit de photons.
Courant d'obscurité (CC) :La valeur du courant sombre pour ce pixel.
t: Temps d'exposition en secondes
σr:Lire le bruit en mode caméra.
Rapport signal/bruit pour un courant d'obscurité négligeable
Dans les cas de court (Avec des temps d'exposition < 1 seconde, ainsi que des caméras refroidies et performantes, le bruit du courant d'obscurité sera généralement bien inférieur au bruit de lecture et négligé en toute sécurité.

Les termes sont à nouveau tels que définis ci-dessus, à l'exception du fait que le signal de courant d'obscurité n'a pas besoin d'être calculé et soustrait du signal car il doit être égal à zéro.
Limitations de ces formules et termes manquants
Les formules ci-contre ne fourniront des réponses correctes que pour CCD etcaméras CMOSLes dispositifs EMCCD et intensifiés introduisent des sources de bruit supplémentaires ; ces équations ne peuvent donc pas être utilisées. Pour une équation de rapport signal/bruit plus complète prenant en compte ces contributions et d'autres, voir « Équations de rapport signal/bruit ».
Un autre terme de bruit fréquemment inclus (ou qui l'était) dans les équations de rapport signal/bruit (RSB) est celui de non-uniformité de la photoréponse (PRNU), parfois aussi appelé « bruit de motif fixe » (FPN). Il représente l'irrégularité du gain et de la réponse du signal sur le capteur, qui peut devenir prédominante à des signaux suffisamment élevés, réduisant ainsi le rapport signal/bruit.
Alors que les premiers appareils photo avaient un PRNU suffisamment important pour nécessiter son inclusion, la plupart des appareils photo modernescaméras scientifiquesLe PRNU est suffisamment faible pour que sa contribution soit bien inférieure à celle du bruit de grenaille des photons, surtout après application des corrections embarquées. Il est donc généralement négligé dans les calculs de rapport signal/bruit. Cependant, le PRNU reste important pour certaines caméras et applications, et il est inclus dans l'équation plus avancée du rapport signal/bruit (RSB) par souci d'exhaustivité. Cela signifie que les équations fournies sont utiles pour la plupart des systèmes CCD/CMOS, mais ne doivent pas être considérées comme universelles.
Types de bruit dans les calculs de rapport signal/bruit
Le calcul du rapport signal/bruit ne se limite pas à comparer un signal à une seule valeur de bruit. En pratique, plusieurs sources de bruit indépendantes contribuent au bruit, et leur compréhension est essentielle.
Bruit de grenaille
● Origine : arrivée statistique de photons ou d’électrons.
● Échelles avec la racine carrée du signal.
● Dominant en imagerie photonique limitée (astronomie, microscopie à fluorescence).
Bruit thermique
● On l’appelle également bruit de Johnson-Nyquist, produit par le mouvement des électrons dans les résistances.
● Augmente avec la température et la bande passante.
● Important dans l’électronique et la communication sans fil.
Bruit de courant d'obscurité
● Variation aléatoire du courant d'obscurité dans les capteurs.
● Plus significatif dans les expositions longues ou les détecteurs chauds.
● Réduit en refroidissant le capteur.
Lire le bruit
● Bruit provenant des amplificateurs et de la conversion analogique-numérique.
● Fixe par lecture, donc critique dans les régimes à faible signal.
Bruit de quantification
● Introduit par la numérisation (arrondi à des niveaux discrets).
● Important dans les systèmes à faible profondeur de bits (par exemple, audio 8 bits).
Bruit environnemental/système
● EMI, diaphonie, ondulation de l'alimentation électrique.
● Peut dominer si le blindage/la mise à la terre est médiocre.
Comprendre lequel de ces facteurs est dominant aide à choisir la bonne formule et la bonne méthode d’atténuation.
Erreurs courantes dans le calcul du SNR
Il est facile de trouver de nombreuses méthodes simplifiées pour estimer le rapport signal/bruit en imagerie. Celles-ci sont généralement moins complexes que les équations ci-contre, permettent une dérivation plus facile à partir de l'image elle-même sans nécessiter la connaissance des paramètres de la caméra, comme le bruit de lecture, ou les deux. Malheureusement, il est probable que chacune de ces méthodes soit incorrecte et produise des résultats faussés et inutiles. Il est fortement recommandé d'utiliser les équations ci-contre (ou leur version avancée) dans tous les cas.
Certains des faux raccourcis les plus courants incluent :
1. Comparaison de l'intensité du signal et de l'intensité du bruit de fond, en niveaux de gris. Cette approche vise à évaluer la sensibilité de la caméra, la puissance du signal ou le rapport signal/bruit en comparant l'intensité de crête à l'intensité du bruit de fond. Cette approche est profondément erronée : l'influence du décalage de la caméra peut influencer arbitrairement l'intensité du bruit de fond, tout comme celle du gain, et aucune contribution du bruit, ni du signal ni du bruit de fond, n'est prise en compte.
2. Diviser les pics du signal par l'écart type d'une zone de pixels d'arrière-plan. Ou comparer les valeurs des pics au bruit visuel de fond révélé par un profil de ligne. En supposant que le décalage soit correctement soustrait des valeurs avant division, le principal danger de cette approche réside dans la présence de lumière de fond. Toute lumière de fond domine généralement le bruit des pixels d'arrière-plan. De plus, le bruit du signal d'intérêt, tel que le bruit de grenaille, n'est pas pris en compte.
3. Signal moyen des pixels d'intérêt vs. écart type des valeurs de pixels : Comparer ou observer l'ampleur de la variation d'un signal de crête entre pixels voisins ou images successives est plus proche de la réalité que d'autres méthodes simplifiées, mais il est peu probable qu'elle évite d'autres influences faussant les valeurs, comme une variation du signal non due au bruit. Cette méthode peut également être imprécise en raison du faible nombre de pixels dans la comparaison. Il ne faut pas non plus oublier de soustraire la valeur de décalage.
4、Calcul du SNR sans conversion en unités d'intensité des photoélectrons, ou sans supprimer le décalage : Étant donné que le bruit de tir des photons est généralement la plus grande source de bruit et repose sur la connaissance du décalage et du gain de la caméra pour la mesure, il n'est pas possible d'éviter le calcul en fonction des photoélectrons pour les calculs du SNR.
5. Évaluation du rapport signal/bruit (RSB) à l'œil nu : Bien que l'évaluation ou la comparaison du SNR à l'œil nu puisse être utile dans certaines circonstances, elle présente également des inconvénients inattendus. L'évaluation du SNR des pixels de forte valeur peut être plus difficile que celle des pixels de faible valeur ou d'arrière-plan. Des effets plus subtils peuvent également jouer un rôle : par exemple, des écrans d'ordinateur différents peuvent afficher des images avec un contraste très différent. De plus, l'affichage d'images avec différents niveaux de zoom dans un logiciel peut influencer considérablement l'apparence visuelle du bruit. Ceci est particulièrement problématique lorsqu'on compare des caméras avec des tailles de pixels différentes dans l'espace objet. Enfin, la présence d'un éclairage d'arrière-plan peut rendre toute évaluation visuelle du SNR impossible.
Applications du SNR
Le SNR est une mesure universelle avec de nombreuses applications :
● Enregistrement audio et musical : détermine la clarté, la plage dynamique et la fidélité des enregistrements.
● Communication sans fil : le rapport signal/bruit est directement lié aux taux d'erreur binaire (BER) et au débit de données.
● Imagerie scientifique : en astronomie, la détection d'étoiles faibles sur fond de lueur du ciel nécessite un rapport signal/bruit élevé.
● Équipement médical : les ECG, les IRM et les tomodensitogrammes s'appuient sur un rapport signal/bruit élevé pour distinguer les signaux du bruit physiologique.
● Appareils photo et photographie : les appareils photo grand public et les capteurs CMOS scientifiques utilisent tous deux le rapport signal/bruit pour évaluer les performances en basse lumière.
Améliorer le rapport signal/bruit
Le SNR étant une mesure cruciale, des efforts importants sont déployés pour l'améliorer. Parmi les stratégies possibles, on peut citer :
Approches matérielles
● Utilisez de meilleurs capteurs avec un courant d’obscurité plus faible.
● Appliquer un blindage et une mise à la terre pour réduire les interférences électromagnétiques.
● Détecteurs de refroidissement pour supprimer le bruit thermique.
Approches logicielles
● Appliquez des filtres numériques pour supprimer les fréquences indésirables.
● Utiliser la moyenne sur plusieurs images.
● Utiliser des algorithmes de réduction du bruit dans le traitement d’images ou audio.
Binning de pixels et son effet sur le rapport signal/bruit
L'effet du binning sur le rapport signal/bruit dépend de la technologie de la caméra et du comportement du capteur, car les performances en matière de bruit des caméras binnées et non binnées peuvent varier considérablement.
Les caméras CCD peuvent additionner la charge des pixels adjacents directement sur la puce. Le bruit de lecture n'est généré qu'une seule fois, mais le signal de courant d'obscurité de chaque pixel est également additionné.
La plupart des caméras CMOS effectuent un binning hors puce, ce qui signifie que les valeurs sont d'abord mesurées (et un bruit de lecture introduit), puis sommées numériquement. Le bruit de lecture de ces sommations augmente lorsqu'on multiplie le nombre de pixels sommés par la racine carrée, soit par un facteur 2 pour un binning 2x2.
Comme le comportement du bruit des capteurs peut être compliqué, pour les applications quantitatives, il est conseillé de mesurer le décalage, le gain et le bruit de lecture de la caméra en mode binned, et d'utiliser ces valeurs pour l'équation du rapport signal/bruit.
Conclusion
Le rapport signal sur bruit (RSB) est l'une des mesures les plus importantes en science, ingénierie et technologie. De la définition de la clarté des appels téléphoniques à la détection de galaxies lointaines, le RSB est essentiel à la qualité des systèmes de mesure et de communication. Maîtriser le RSB ne se résume pas à mémoriser des formules : il s'agit de comprendre les hypothèses, les limites et les compromis possibles en situation réelle. Grâce à cette perspective, les ingénieurs et les chercheurs peuvent réaliser des mesures plus fiables et concevoir des systèmes qui extraient des informations pertinentes, même dans des conditions de bruit.
Envie d'en savoir plus ? Consultez les articles connexes :
Tucsen Photonics Co., Ltd. Tous droits réservés. Veuillez citer la source pour toute citation.www.tucsen.com

 25/09/11
25/09/11